Learning Compiler 4 Finite Automata

Note

Specifying Lexical Structure Using Regular Expressions

Union: $A|B\equiv A + B$
Option: $A + \epsilon \equiv A?$
Range: $'a'+'b'+\dots+'z'\equiv [a-z]$
Excluded range: complement of $[a-z] \equiv [\hat{}a-z]$

Regular Expressions => Lexical Spec.

1. Write a rexp for the lexemes of each token
2. Construct $R$, matching all lexemes for all tokens
   • $R = \text{Keyword} + \text{Identifier} + \text{Number} + \dots \\ = R_1 + R_2 + \dots$
3. Let input be $x_1\dots x_n$
   • For $1 \leq i \leq n$ check $x_1\dots x_i\in L(R)$
4. If success, then we know that $x_1\dots x_i\in L(R_j)$ for some $j$
5. Remove $x_1\dots x_i$ from input and go to (3)

Ambiguities

Rule: Pick longest possible string in $L(R)$

Rule: Use rule listed first

Error handling

No rule matches a prefix of input

Solution:

• Write a rule matching all “bad” strings
• Put it last (lowest priority)

Summary

Regular expressions provide a concise notation for string patterns

Use in lexical analysis requires small extensions

• To resolve ambiguities
• To handle errors

Good algorithms known

• Require only single pass over the input
• Few operations per character (table lookup)

Finite Automata

Regular expressions = specification

Finite automata = implementation

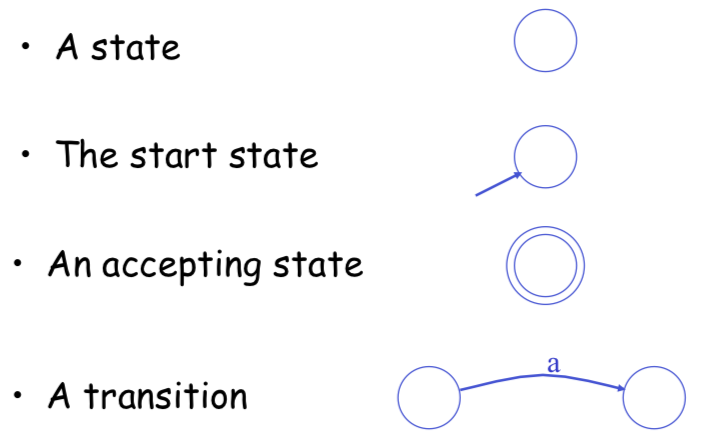
A finite automaton consists of – An input alphabet $\Sigma$

• A set of states $S$
• A start state $n$
• A set of accepting states $F\subseteq S$
• A set of transitions state $\rightarrow^{\text{input}}$ state

Transition: $s_1 \rightarrow^{a} s_2$

Is read: In state $s_1$ on input “a” go to state $s_2$

If end of input and in accepting state => accept

Otherwise => reject

Finite Automata State Graphs

Epsilon Moves

$\epsilon$-moves

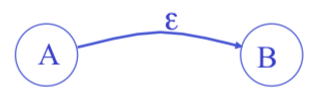
Machine can move from state A to state B without reading input

Deterministic and Nondeterministic Automata

Deterministic Finite Automata (DFA)

• One transition per input per state
• No $\epsilon$-moves

Nondeterministic Finite Automata (NFA)

• Can have multiple transitions for one input in a
  given state
• Can have $\epsilon$-moves

Execution of Finite Automata

A DFA can take only one path through the state graph

• Completely determined by input

NFAs can choose

• Whether to make $\epsilon$-moves
• Which of multiple transitions for a single input to take

Acceptance of NFAs

An NFA can get into multiple states

Rule: NFA accepts if it can get to a final state

NFA vs. DFA

NFAs and DFAs recognize the same set of languages (regular languages)

DFAs are faster to execute

• No choices to consider

For a given language NFA can be simpler than DFA

DFA can be exponentially larger than NFA

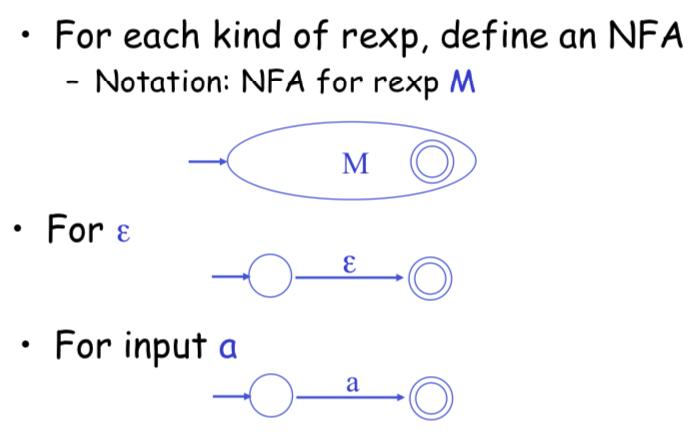
Regular Expressions to Finite Automata

High-level sketch:

Lexical Specification -> Regular Expressions -> NFA -> DFA -> Table-driven Implementation of DFA

Regular Expressions to NFA

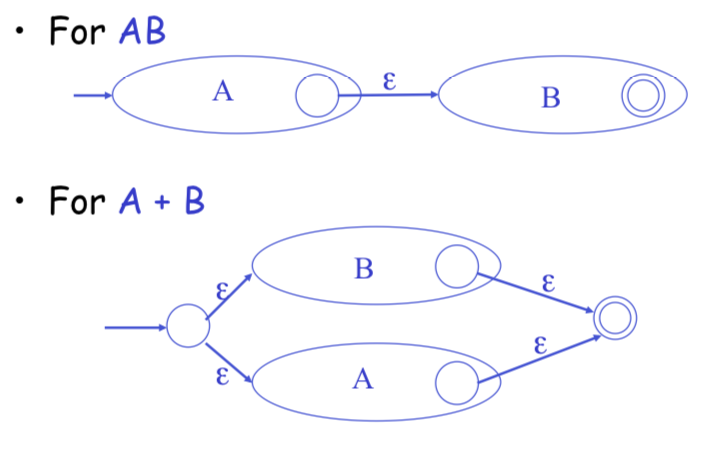
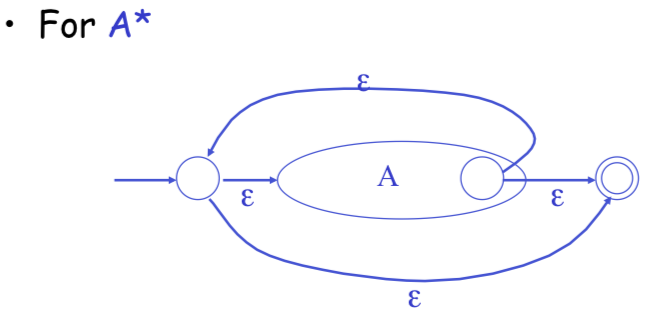
NFA to DFA: The Trick

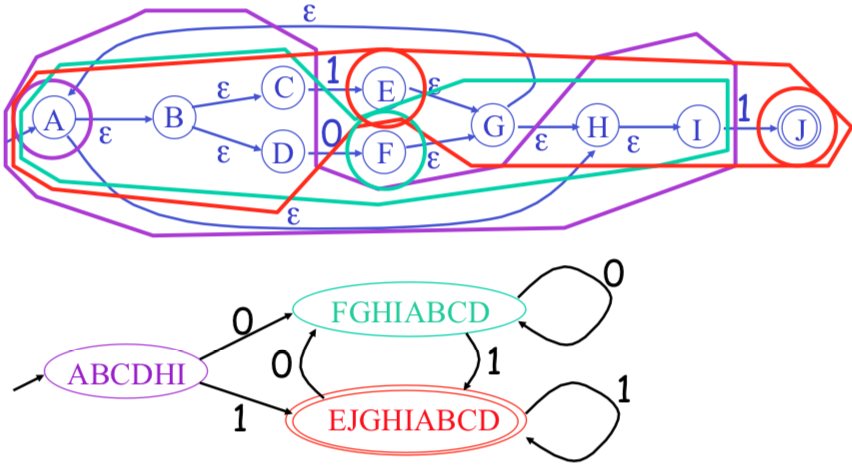
Simulate the NFA

Each state of DFA = a non-empty subset of states of the NFA

Start state = the set of NFA states reachable through $\epsilon$-moves from NFA start state

Add a transition $S \rightarrow^a S'$ to DFA iff $S'$ is the set of NFA states reachable from any
state in $S$ after seeing the input $a$, considering $\epsilon$-moves as well

NFA to DFA. Remark

An NFA may be in many states at any time

If there are N states, the NFA must be in some subset of those N states

How many subsets are there?

• $2^N - 1$ = finitely many

Example

Implementation

A DFA can be implemented by a 2D table T

• One dimension is “states”
• Other dimension is “input symbol”
• For every transition $S_i \rightarrow^a S_k$ define $T[i, a] = k$

DFA “execution”

• If in state $S_i$ and input $a$, read $T[i, a] = k$ and skip to state $S_k$
• Very efficient

NFA -> DFA conversion is at the heart of tools such as flex

DFAs can be huge

In practice, flex-like tools trade off speed for space in the choice of NFA and DFA representations

Reference

Slides: Finite Automata

Video: Compiler Stanford 2014